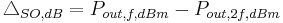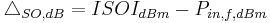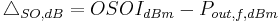Second-order intercept point
The Second Order Intercept Point, also known as the SOI, IP2, or IIP2 (Input Intercept Point), is a measure of linearity that quantifies the second-order distortion generated by nonlinear systems and devices. Examples of frequently used devices that are concerned with this measure are amplifiers and mixers. It is related to the third-order intercept point, which is generally used for quantifying degree of nonlinearity of a nonlinear system or it can also be used to estimate the nonlinear products present at the output of such a system.
Contents |
Definition
At low power levels, the fundamental output power rises in a one-to-one ratio (in terms of dB) of the input power, while the second-order output power rises in a two-to-one ratio . When the input power is high enough and the device reaches saturation, the output power flattens out in both the first- and second-order cases.
The second order intercept point is the output power point at which the extrapolated first- and second-order lines intersect on a plot, since the actual power levels will flatten off due to saturation at much lower power level typically. In other words, the response is assumed to be perfect all the way to infinity. There are actually values for both the input and output SOI (known as the ISOI & OSOI) of a device or system, being related by the gain of the device or system. The OSOI in dB is simply the ISOI in dB plus the gain of the device or system.
Derivation
To determine the second-order characteristics of a device, a strong signal is put through the device, and the outputs are measured. Both single- and two-tone techniques can be used, and while there will be frequencies components off to infinity, for SOI analysis the fundamental and second-order distortion products are the desired results.
Single-tone analysis
In single-tone analysis, one tone at the desired frequency is generated and put through the device. There will be output at the fundamental, and the output due to second-order effects will be at DC and twice the input frequency. The derivation follows:
Two-tone analysis
Single-tone analysis fails to illustrate several common linearity problems, therefore in two-tone analysis, two tones of approximately equal strength are put through the device. There will be output at the fundamental frequencies, and the output due to second-order effects will be at DC, twice the input frequencies, and the sum and difference of the input frequencies. The derivation follows:
Cascade gain
If multiple devices are connected in cascade, and their individual ISOI and OSOI are known, it is possible to calculate the ISOI and OSOI of the entire system. It is helpful to think of how they are derived in the following ways. For the ISOI, the second-order distortion components can be "moved" to the beginning of the cascade, where the ISOI of the first component is unaffected by any gain, the ISOI of the second component is divided by the gain of the first component, and this process continues to the end of the cascade. In this case the gain of the last device has no effect on the cascade ISOI.
In the OSOI case, a similar process can be performed, except the distortion components are moved to the end of the cascade. Here, the OSOI of the first device is affected by the gain of all subsequent devices, and so on. For the OSOI, the gain of the first device has no effect on the cascade OSOI.
Both coherent and non-coherent derivations of these equations exist, due to the possible phase differences of the distortion components. In the coherent case, all of the components are exactly in phase, and their voltages simply add, while in the non-coherent case the phases are random and the distortion powers add together. The coherent case represents the most conservative (i.e worst-case) answer, and the non-coherent case is generally a more accurate description for most systems.
Coherent SOI cascade equations
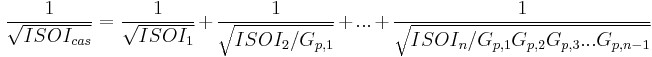
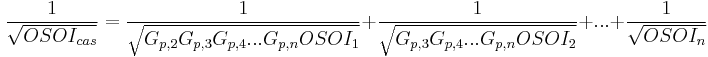
Non-Coherent SOI cascade equations
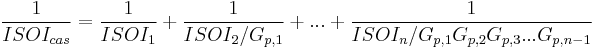
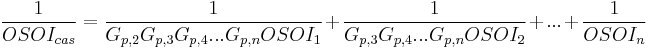
Useful second order equations
In the following equations f refers to the fundamental frequency, and 2f refers to the second-order distortion component frequencies.
- OSOIdBm = ISOIdBm+GdB
- Pout,f,dBm = Pin,f,dBm - ISOIdBm + OSOIdBm
- Pout,2f,dBm = 2Pin,f,dBm - 2ISOIdBm + OSOIdBm
- Pin,2f,dBm = 2Pin,f,dBm - ISOIdBm
- Pout,2f,dBm = 2Pout,f,dBm - OSOIdBm
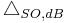 is the difference in power between the fundamental output and the output of the second-order components, as shown on the figure to the right.
is the difference in power between the fundamental output and the output of the second-order components, as shown on the figure to the right.
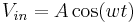
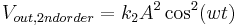
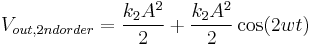
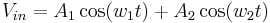
![V_{out,2nd order} = k_{2}[A_{1}\cos(w_{1}t) %2B A_{2}\cos(w_{2}t)]^{2}](/2012-wikipedia_en_all_nopic_01_2012/I/e5efb42c877cc51d641c7c3ac8ad2a9d.png)
![V_{out,2nd order} = k_{2}\{\frac{A_{1}^{2} %2B A_{2}^{2}}{2} %2B \frac{A_{1}^{2}\cos(2w_{1}t)}{2} %2B \frac{A_{2}^{2}\cos(2w_{2}t)}{2} %2B A_{1}A_{2}\cos[(w_{1}%2Bw_{2})t] %2B A_{1}A_{2}\cos[(w_{1}-w_{2})t] \}](/2012-wikipedia_en_all_nopic_01_2012/I/2626fe899ca02c816999e9cd12fccbfb.png)